开始之前

本人对各种渲染技术很感兴趣，但由于现实原因不能深入探索。对Unity中预计算大气渲染技术研究是出于爱好，在课余业余时间自学的，仅仅是阅读到刚刚能看懂个大概的水平。我觉得从理论/物理，到数学公式，再到代码的过程十分神奇，我的学习过程就是通过代码的实现，反推其中的几何/物理原理。尽管我是自学，并没有深厚的学术背景，但通过反向工程和参考各种资源，我逐渐拼凑出了大气散射的复杂机制及其实现方式。

参考的Unity项目仓库：https://github.com/Scrawk/Brunetons-Improved-Atmospheric-Scattering

参考的散射原理（后期看到多次散射才找到ebruneton的原文）：

• https://ebruneton.github.io/precomputed_atmospheric_scattering/atmosphere/functions.glsl.html

• https://youtu.be/DxfEbulyFcY?si=rCxfRidhp1PmpGh2

本篇内容

// 计算透射度材质
            compute.Dispatch(compute_transmittance, CONSTANTS.TRANSMITTANCE_WIDTH / NUM_THREADS, CONSTANTS.TRANSMITTANCE_HEIGHT / NUM_THREADS, 1);
            // 计算没有经过任何散射的地面直接辐照度
            compute.Dispatch(compute_direct_irradiance, CONSTANTS.IRRADIANCE_WIDTH / NUM_THREADS, CONSTANTS.IRRADIANCE_HEIGHT / NUM_THREADS, 1);
            // 计算3D单次散射纹理
            for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer) 
            {
                // 计算3D texture ScatteringArray
                compute.SetInt("layer", layer);
                compute.Dispatch(compute_single_scattering, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
            }
            // 循环计算多次散射
            for (int scattering_order = 2; scattering_order <= num_scattering_orders; ++scattering_order) 
            {
                // 计算大气辐射度
                for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer) 
                {
                    compute.SetInt("layer", layer);
                    compute.Dispatch(compute_scattering_density, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
                }
                // 计算来自地面的辐照度
                compute.Dispatch(compute_indirect_irradiance, CONSTANTS.IRRADIANCE_WIDTH / NUM_THREADS, CONSTANTS.IRRADIANCE_HEIGHT / NUM_THREADS, 1);
                // 利用上面两项计算出本阶的多次散射
                for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer) 
                {
                    compute.SetInt("layer", layer);
                    compute.Dispatch(compute_multiple_scattering, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
                }
            }

本篇主要讲解

• 各种常量

• 上面代码中的第一阶段——计算透射度材质

各常量解析

CIE_2_DEG_COLOR_MATCHING_FUNCTIONS

// Values from "CIE (1931) 2-deg color matching functions"
public static readonly double[] CIE_2_DEG_COLOR_MATCHING_FUNCTIONS = new double[]
{
    360, 0.000129900000, 0.000003917000, 0.000606100000,
    365, 0.000232100000, 0.000006965000, 0.001086000000,
    370, 0.000414900000, 0.000012390000, 0.001946000000,
    375, 0.000741600000, 0.000022020000, 0.003486000000,
    380, 0.001368000000, 0.000039000000, 0.006450001000,
    385, 0.002236000000, 0.000064000000, 0.010549990000,
    390, 0.004243000000, 0.000120000000, 0.020050010000,
    // …（中间数据省略）
    800, 0.000010253980, 0.000003702900, 0.000000000000,
    805, 0.000007221456, 0.000002607800, 0.000000000000,
    810, 0.000005085868, 0.000001836600, 0.000000000000,
    815, 0.000003581652, 0.000001293400, 0.000000000000,
    820, 0.000002522525, 0.000000910930, 0.000000000000,
    825, 0.000001776509, 0.000000641530, 0.000000000000,
    830, 0.000001251141, 0.000000451810, 0.000000000000,
};

数组中每4个元素描述不同波长(从360 nm到830 nm)下的三个颜色匹配函数的值x̅(λ)、y̅(λ) 和 z̅(λ) 。CIE 1931 2° 标准观察者颜色匹配函数中的 x̅(λ)、y̅(λ) 和 z̅(λ) 分别代表了人眼在不同波长光下对三种“假想原色”刺激的敏感程度。

这是通过大量的视觉匹配实验，使用一个 2° 的视野角，确定了人眼如何混合不同光谱的光以匹配某个参考光色。实验中受试者用三个不同的光源（称作原色刺激）来匹配不同波长的单色光。为了满足任何光谱混合都能用三个数值准确描述的要求，人类视觉系统所呈现的感知被重新定义为一组数学上构造的“虚拟原色” X、Y、Z，而这些虚拟原色不是物理上存在的光，而是经过一定变换后的结果。

• x̅(λ)
  这个函数描述了在特定波长λ下，人眼对“X 原色”的响应权重。X 通常与红光成分较为相关，但它是经过数学构造用以补偿人眼对颜色敏感度不均的部分。

• y̅(λ)
  这个函数与亮度（或称明度）密切相关。Y 函数被精心选择以近似人眼在明亮环境下的亮度感受函数，所以它代表了光源的亮度信息。当我们计算光源的“明度”时，实际上是对光谱加权 y̅(λ) 后得到的积分值。

• z̅(λ)
  z̅(λ) 则描述了在特定波长下对“Z 原色”的响应，这一分量主要补充了 X 和 Y 无法覆盖的蓝色及紫色部分。Z 的引入确保了 CIE XYZ 色彩空间能够涵盖人眼可见光谱的全貌。

XYZ_TO_SRGB

// The conversion matrix from XYZ to linear sRGB color spaces.
// Values from https://en.wikipedia.org/wiki/SRGB.
public static readonly double[] XYZ_TO_SRGB = new double[]
{
    +3.2406, -1.5372, -0.4986,
    -0.9689, +1.8758, +0.0415,
    +0.0557, -0.2040, +1.0570
};

这个3×3矩阵用于将线性 XYZ 颜色空间的值转换为线性 sRGB 颜色空间，转换矩阵的数值取自 Wikipedia 上关于 sRGB 的标准描述。转换过程中可能还会加入伽玛校正以得到最终的显示结果。

https://en.wikipedia.org/wiki/SRGB

距离/角度相关

static readonly float kSunAngularRadius = 0.00935f / 2.0f;
static readonly float kBottomRadius = 6360000.0f;
static readonly float kLengthUnitInMeters = 1000.0f;
double max_sun_zenith_angle = (UseHalfPrecision ? 102.0 : 120.0) / 180.0 * Mathf.PI;

• kSunAngularRadius : 太阳的角半径（除以2后），用于描述太阳在天空中的视角大小。

  • 角直径与角半径
    天文中描述一个天体在天空中的大小时，常用到“角直径”这个概念。角直径指的是从观察者视点看到天体两个边缘之间形成的角度。例如，太阳的角直径大约为 0.00935 弧度（约 0.53°）。
    角半径 则是角直径的一半，表示从天体中心到边缘所占用的角度。

• kBottomRadius : 地球的半径，也是大气层下界

• kLengthUnitInMeters : 1 单位 = 1000 米，便于缩放计算

• max_sun_zenith_angle : 太阳光顶角的最大余弦值，在此角度下大气散射仍然有效。必须预先计算（为了获得最大的精度，需要使用最合适的最小的太阳高度角）。例如，对于地球情况，102° 是一个不错的选择，此时 mu_s_min = -0.2）。

太阳辐照度数据

double[] kSolarIrradiance = new double[]
{
    1.11776, 1.14259, 1.01249, 1.14716, 1.72765, 1.73054, 1.6887, 1.61253,
    1.91198, 2.03474, 2.02042, 2.02212, 1.93377, 1.95809, 1.91686, 1.8298,
    1.8685, 1.8931, 1.85149, 1.8504, 1.8341, 1.8345, 1.8147, 1.78158, 1.7533,
    1.6965, 1.68194, 1.64654, 1.6048, 1.52143, 1.55622, 1.5113, 1.474, 1.4482,
    1.41018, 1.36775, 1.34188, 1.31429, 1.28303, 1.26758, 1.2367, 1.2082,
    1.18737, 1.14683, 1.12362, 1.1058, 1.07124, 1.04992
};

https://www2.nrel.gov/grid/solar-resource/spectra-am1.5

数组中的每个值代表一个波段(每个波段宽度为 10nm)内的太阳辐照度，值的单位是 W/m²（瓦每平方米）

这些辐照度数据摘自 ASTM G-173 标准光谱，这是一个公认的标准数据集，通常用于精确描述太阳光谱在地表附近（标准大气条件下）的分布。

臭氧截面数据

https://www.iup.uni-bremen.de/gruppen/molspec/databases/referencespectra/o3spectra2011/index.html

double[] kOzoneCrossSection = new double[]
{
    1.18e-27, 2.182e-28, 2.818e-28, 6.636e-28, 1.527e-27, 2.763e-27, 5.52e-27,
    8.451e-27, 1.582e-26, 2.316e-26, 3.669e-26, 4.924e-26, 7.752e-26, 9.016e-26,
    1.48e-25, 1.602e-25, 2.139e-25, 2.755e-25, 3.091e-25, 3.5e-25, 4.266e-25,
    4.672e-25, 4.398e-25, 4.701e-25, 5.019e-25, 4.305e-25, 3.74e-25, 3.215e-25,
    2.662e-25, 2.238e-25, 1.852e-25, 1.473e-25, 1.209e-25, 9.423e-26, 7.455e-26,
    6.566e-26, 5.105e-26, 4.15e-26, 4.228e-26, 3.237e-26, 2.451e-26, 2.801e-26,
    2.534e-26, 1.624e-26, 1.465e-26, 2.078e-26, 1.383e-26, 7.105e-27
};

数组中每个值表示臭氧（O₃）在特定 10nm 波段内的光学截面，单位为 m²（平方米）。

“截面”描述的是一个分子或原子与光子相互作用（吸收或散射）的概率，单位一般是平方米（m²）。数值越大，表示该波段内光子与臭氧分子发生相互作用的可能性越高。臭氧对光的吸收能力与波长非常相关，尤其是在紫外区域，臭氧截面会显著增大，从而有效地吸收进入大气层的紫外光。臭氧在约254 nm的波长处具有强烈的吸收峰，这是臭氧层吸收紫外-C辐射的关键区域。​在更长波长的紫外-B区域（约280–315 nm），臭氧的吸收能力仍然显著，但不如UV-C区域强烈。​

计算臭氧密度

// From https://en.wikipedia.org/wiki/Dobson_unit, in molecules.m^-2.
double kDobsonUnit = 2.687e20;
// Maximum number density of ozone molecules, in m^-3 (computed so at to get
// 300 Dobson units of ozone - for this we divide 300 DU by the integral of
// the ozone density profile defined below, which is equal to 15km).
double kMaxOzoneNumberDensity = 300.0 * kDobsonUnit / 15000.0;

DU 等于 2.687×10^20 个臭氧分子每平方米，即如果将臭氧在一个垂直大气柱中全部压缩到标准状况下，厚度大约为 0.01 毫米。
在代码中，kDobsonUnit 被定义为 2.687e20，表示每 1 DU 的臭氧分子的数量。

MaxOzoneNumberDensity : 臭氧的最大分子数密度。表示假设 300 DU 均匀分布在 15 公里（15000 米）的厚度中，得到平均臭氧分子的数密度。

大气密度剖面

// An atmosphere layer of width 'width', and whose density is defined as
//   'exp_term' * exp('exp_scale' * h) + 'linear_term' * h + 'constant_term',
// clamped to [0,1], and where h is the altitude.
struct DensityProfileLayer {
  Length width;
  Number exp_term;
  InverseLength exp_scale;
  InverseLength linear_term;
  Number constant_term;
};

一个宽度为'width'的大气层，其密度定义为
'exp_term' * exp('exp_scale' * h) + 'linear_term' * h + 'constant_term'，
并且被限制在[0,1]范围内，其中 h 是海拔。

下面是各个密度层的定义：

double kRayleighScaleHeight = 8000.0;
double kMieScaleHeight = 1200.0;

DensityProfileLayer rayleigh_layer = new DensityProfileLayer("rayleigh", 0.0, 1.0, -1.0 / kRayleighScaleHeight, 0.0, 0.0);
DensityProfileLayer mie_layer = new DensityProfileLayer("mie", 0.0, 1.0, -1.0 / kMieScaleHeight, 0.0, 0.0);

// Density profile increasing linearly from 0 to 1 between 10 and 25km, and
// decreasing linearly from 1 to 0 between 25 and 40km. This is an approximate
// profile from http://www.kln.ac.lk/science/Chemistry/Teaching_Resources/
// Documents/Introduction%20to%20atmospheric%20chemistry.pdf (page 10).
List<DensityProfileLayer> ozone_density = new List<DensityProfileLayer>();
ozone_density.Add(new DensityProfileLayer("absorption0", 25000.0, 0.0, 0.0, 1.0 / 15000.0, -2.0 / 3.0));
ozone_density.Add(new DensityProfileLayer("absorption1", 0.0, 0.0, 0.0, -1.0 / 15000.0, 8.0 / 3.0));

预计算常量

double kTopRadius = 6420000.0;
double kRayleigh = 1.24062e-6;
double kMieAngstromAlpha = 0.0;
double kMieAngstromBeta = 5.328e-3;
double kMieSingleScatteringAlbedo = 0.9;
double kMiePhaseFunctionG = 0.8;
double kGroundAlbedo = 0.1;

List<double> wavelengths = new List<double>();
List<double> solar_irradiance = new List<double>();
List<double> rayleigh_scattering = new List<double>();
List<double> mie_scattering = new List<double>();
List<double> mie_extinction = new List<double>();
List<double> absorption_extinction = new List<double>();
List<double> ground_albedo = new List<double>();

for (int l = kLambdaMin; l <= kLambdaMax; l += 10)
{
    double lambda = l * 1e-3;  // micro-meters
    double mie = kMieAngstromBeta / kMieScaleHeight * Math.Pow(lambda, -kMieAngstromAlpha);

    wavelengths.Add(l);

    solar_irradiance.Add(kSolarIrradiance[(l - kLambdaMin) / 10]);

    rayleigh_scattering.Add(kRayleigh * Math.Pow(lambda, -4));
    mie_scattering.Add(mie * kMieSingleScatteringAlbedo);
    mie_extinction.Add(mie);
    absorption_extinction.Add(UseOzone ? kMaxOzoneNumberDensity * kOzoneCrossSection[(l - kLambdaMin) / 10] : 0.0);
    ground_albedo.Add(kGroundAlbedo);
}

Note：Rayleigh 散射理论指出，当散射粒子的尺寸远小于入射光波长时（例如大气中的气体分子），散射截面与波长的四次方成反比。

直接解析的 Mie 理论计算十分复杂，因此工程中常采用经验公式近似描述散射系数的波长依赖性。其中一种常用的方法就是应用 Angstrom 公式：

double max_sun_zenith_angle = (UseHalfPrecision ? 102.0 : 120.0) / 180.0 * Mathf.PI; 指的是太阳位置与垂直方向之间的角度。

在大气渲染时，往往会考虑到太阳低于地平线的情况（例如日落后的一段时间，这个时候太阳与地面的法线夹角大概是90°），但太阳本身有大小，所以当中心点过了90°时还有部分露在上面，因此允许天顶角超过 90°。

常量赋值

m_model = new Model();

m_model.HalfPrecision = UseHalfPrecision;
m_model.CombineScatteringTextures = UseCombinedTextures;
m_model.UseLuminance = UseLuminance;
m_model.Wavelengths = wavelengths;
m_model.SolarIrradiance = solar_irradiance;
m_model.SunAngularRadius = kSunAngularRadius;
m_model.BottomRadius = kBottomRadius;
m_model.TopRadius = kTopRadius;
m_model.RayleighDensity = rayleigh_layer;
m_model.RayleighScattering = rayleigh_scattering;
m_model.MieDensity = mie_layer;
m_model.MieScattering = mie_scattering;
m_model.MieExtinction = mie_extinction;
m_model.MiePhaseFunctionG = kMiePhaseFunctionG;
m_model.AbsorptionDensity = ozone_density;
m_model.AbsorptionExtinction = absorption_extinction;
m_model.GroundAlbedo = ground_albedo;
m_model.MaxSunZenithAngle = max_sun_zenith_angle;
m_model.LengthUnitInMeters = kLengthUnitInMeters;

Note： kMiePhaseFunctionG 是在 Mie 散射相函数中用来描述散射方向性（或称为各向异性）的一个参数，通常称为“渐近因子”或“偏斜因子"。

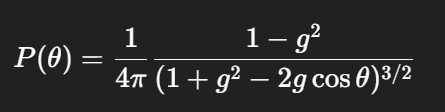
Henyey-Greenstein (HG) 相函数（入射光线方向和散射光线方向有夹角θ，散射值与这个夹角有关，这部分被提取出来叫做相函数）中，θ 是散射角，而 g 就是 kMiePhaseFunctionG，表示平均散射角的余弦值。

预计算天空和太阳的IrradianceToLuminance

private static void ComputeSpectralRadianceToLuminanceFactors(IList<double> wavelengths, IList<double> solar_irradiance, double lambda_power, out double k_r, out double k_g, out double k_b) 
{
    k_r = 0.0;
    k_g = 0.0;
    k_b = 0.0;
    double solar_r = Interpolate(wavelengths, solar_irradiance, kLambdaR);
    double solar_g = Interpolate(wavelengths, solar_irradiance, kLambdaG);
    double solar_b = Interpolate(wavelengths, solar_irradiance, kLambdaB);
    int dlambda = 1;

    for (int lambda = kLambdaMin; lambda < kLambdaMax; lambda += dlambda) 
    {
        // 
        double x_bar = SampleCIEColorMatchingFunction(lambda, 1);
        double y_bar = SampleCIEColorMatchingFunction(lambda, 2);
        double z_bar = SampleCIEColorMatchingFunction(lambda, 3);

        double[] xyz2srgb = CONSTANTS.XYZ_TO_SRGB;
        double r_bar = xyz2srgb[0] * x_bar + xyz2srgb[1] * y_bar + xyz2srgb[2] * z_bar;
        double g_bar = xyz2srgb[3] * x_bar + xyz2srgb[4] * y_bar + xyz2srgb[5] * z_bar;
        double b_bar = xyz2srgb[6] * x_bar + xyz2srgb[7] * y_bar + xyz2srgb[8] * z_bar;
        double irradiance = Interpolate(wavelengths, solar_irradiance, lambda);

        k_r += r_bar * irradiance / solar_r * Math.Pow(lambda / kLambdaR, lambda_power);
        k_g += g_bar * irradiance / solar_g * Math.Pow(lambda / kLambdaG, lambda_power);
        k_b += b_bar * irradiance / solar_b * Math.Pow(lambda / kLambdaB, lambda_power);
    }

    k_r *= CONSTANTS.MAX_LUMINOUS_EFFICACY * dlambda;
    k_g *= CONSTANTS.MAX_LUMINOUS_EFFICACY * dlambda;
    k_b *= CONSTANTS.MAX_LUMINOUS_EFFICACY * dlambda;
}

在函数开头，通过 Interpolate 函数分别获得在预定义的参考波长（kLambdaR、kLambdaG、kLambdaB）上的太阳辐照度。

然后通过一个 for 循环，从 kLambdaMin 到 kLambdaMax（波长范围）以每1nm（dlambda = 1）的步长进行积分，累加每个波长对亮度转换因子贡献的部分。对于每个波长 lambda，调用 SampleCIEColorMatchingFunction(lambda, index) 得到 CIE 1931 标准观察者的颜色匹配函数：x_bar, y_bar, z_bar 分别对应不同颜色通道在 XYZ 三刺激值中的响应。

再将 (x̅, y̅, z̅) （x_bar, y_bar, z_bar）转换成 (r_bar, g_bar, b_bar)，这三个值给出了在该波长下，对应 RGB 颜色分量的权重。

用 Interpolate 获取当前波长 lambda 对应的太阳辐照度 irradiance。

irradiance / solar_channel是为了归一化当前波长与参考波长下的太阳辐照度。

Math.Pow(lambda / kLambdaX, lambda_power); 是额外的权重项，用 lambda_power 调整每个波长的贡献，可能用来控制预计算时的数值范围或其他校正目的。

在积分完成后，将每个颜色通道的累积分数乘以：CONSTANTS.MAX_LUMINOUS_EFFICACY×dlambda

private void SkySunRadianceToLuminance(out Vector3 skySpectralRadianceToLuminance, out Vector3 sunSpectralRadianceToLuminance)
{
    bool precompute_illuminance = NumPrecomputedWavelengths > 3;
    double sky_k_r, sky_k_g, sky_k_b;

    if (precompute_illuminance)
        sky_k_r = sky_k_g = sky_k_b = CONSTANTS.MAX_LUMINOUS_EFFICACY;
    else
        ComputeSpectralRadianceToLuminanceFactors(Wavelengths, SolarIrradiance, -3, out sky_k_r, out sky_k_g, out sky_k_b);

    // Compute the values for the SUN_RADIANCE_TO_LUMINANCE constant.
    double sun_k_r, sun_k_g, sun_k_b;
    ComputeSpectralRadianceToLuminanceFactors(Wavelengths, SolarIrradiance, 0, out sun_k_r, out sun_k_g, out sun_k_b);

    skySpectralRadianceToLuminance = new Vector3((float)sky_k_r, (float)sky_k_g, (float)sky_k_b);
    sunSpectralRadianceToLuminance = new Vector3((float)sun_k_r, (float)sun_k_g, (float)sun_k_b);
}

然后通过这个函数获取到 skySpectralRadianceToLuminance 和 sunSpectralRadianceToLuminance

Wikipedia里有完整的介绍：https://en.wikipedia.org/wiki/Luminous_efficiency_function

但代码中实际上的计算公式是：

也许两者之间有什么相关性

第一阶段：预计算大气透射度 Transmittance

下面是预计算大气渲染的第一阶段，计算 Transmittance Texture

#pragma kernel ComputeTransmittance
[numthreads(NUM_THREADS,NUM_THREADS,1)]
void ComputeTransmittance(uint3 id : SV_DispatchThreadID)
{
    float2 gl_FragCoord = id.xy + float2(0.5,0.5);
    transmittanceWrite[id.xy] = float4(ComputeTransmittanceToTopAtmosphereBoundaryTexture(gl_FragCoord), 1);
}

DimensionlessSpectrum ComputeTransmittanceToTopAtmosphereBoundaryTexture(float2 gl_frag_coord) 
{
  const float2 TRANSMITTANCE_TEXTURE_SIZE = float2(TRANSMITTANCE_TEXTURE_WIDTH, TRANSMITTANCE_TEXTURE_HEIGHT);
  Length r;
  Number mu;
  GetRMuFromTransmittanceTextureUv(gl_frag_coord / TRANSMITTANCE_TEXTURE_SIZE, r, mu);
  return ComputeTransmittanceToTopAtmosphereBoundary(r, mu);
}

GetRMuFromTransmittanceTextureUv

首先看这个函数，通过r和mu映射到纹理坐标0-1。

Number GetUnitRangeFromTextureCoord(Number u, int texture_size) {
  return (u - 0.5 / Number(texture_size)) / (1.0 - 1.0 / Number(texture_size));
}

更确切的说是映射到 0.5 ~ 纹理大小-1/2 ，这样可以映射到像素中心

这是反映射：

Number GetTextureCoordFromUnitRange(Number x, int texture_size) {
  return 0.5 / Number(texture_size) + x * (1.0 - 1.0 / Number(texture_size));
}

以下函数就从纹理坐标映射到0~1，然后计算r和mu，用于后续的Transmittance计算

void GetRMuFromTransmittanceTextureUv(float2 uv, out Length r, out Number mu) 
{

  Number x_mu = GetUnitRangeFromTextureCoord(uv.x, TRANSMITTANCE_TEXTURE_WIDTH);
  Number x_r = GetUnitRangeFromTextureCoord(uv.y, TRANSMITTANCE_TEXTURE_HEIGHT);
  // Distance to top atmosphere boundary for a horizontal ray at ground level.
  Length H = sqrt(top_radius * top_radius - bottom_radius * bottom_radius);
  // Distance to the horizon, from which we can compute r:
  Length rho = H * x_r;
  r = sqrt(rho * rho + bottom_radius * bottom_radius);
  Length d_min = top_radius - r;
  Length d_max = rho + H;
  Length d = d_min + x_mu * (d_max - d_min);
  mu = d == 0.0 * m ? Number(1.0) : (H  H - rho  rho - d  d) / (2.0  r  d);
  mu = ClampCosine(mu);
}

我对这部分代码进行反向几何解析，画出了这张图：

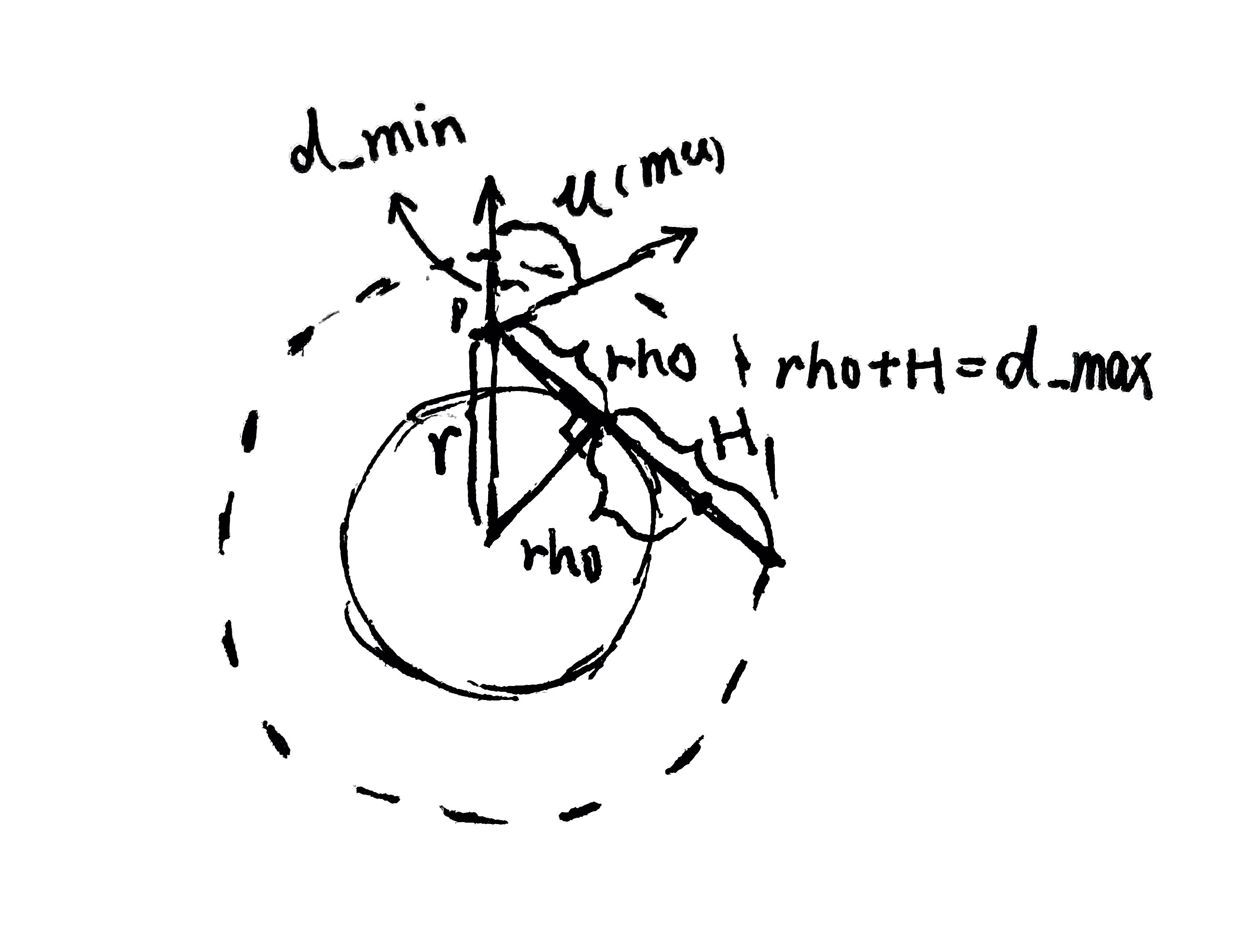
这是摘自Bruneton的原文的图片：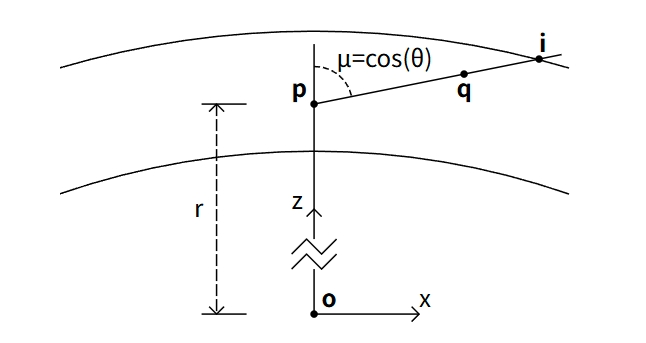

float2 GetTransmittanceTextureUvFromRMu(Length r, Number mu) 
{
  // Distance to top atmosphere boundary for a horizontal ray at ground level.
  Length H = sqrt(top_radius * top_radius - bottom_radius * bottom_radius);
  // Distance to the horizon.
  Length rho = SafeSqrt(r * r - bottom_radius * bottom_radius);
  // Distance to the top atmosphere boundary for the ray (r,mu), and its minimum
  // and maximum values over all mu - obtained for (r,1) and (r,mu_horizon).
  Length d = DistanceToTopAtmosphereBoundary(r, mu);
  Length d_min = top_radius - r;
  Length d_max = rho + H;
  Number x_mu = (d - d_min) / (d_max - d_min);
  Number x_r = rho / H;
  return float2(GetTextureCoordFromUnitRange(x_mu, TRANSMITTANCE_TEXTURE_WIDTH),
                GetTextureCoordFromUnitRange(x_r, TRANSMITTANCE_TEXTURE_HEIGHT));
}

这是从r、mu映射到0-1的结果，关键在于DistanceToTopAtmosphereBoundary函数：

Length DistanceToTopAtmosphereBoundary(Length r, Number mu) 
{
  Area discriminant = r * r * (mu * mu - 1.0) + top_radius * top_radius;
  return ClampDistance(-r * mu + SafeSqrt(discriminant));
}

原理是解二次方程，用判别式求解：

其中P是所在点，v是方向向量，v与法线方向夹角为θ

判断是否与地面相交

Length DistanceToBottomAtmosphereBoundary(Length r, Number mu) 
{
  Area discriminant = r * r * (mu * mu - 1.0) + bottom_radius * bottom_radius;
  return ClampDistance(-r * mu - SafeSqrt(discriminant));
}

bool RayIntersectsGround(Length r, Number mu) 
{
  return mu < 0.0 && r * r * (mu * mu - 1.0) + bottom_radius * bottom_radius >= 0.0 * m2;
}

原理也是与上面的二次方程一样，只不过把 top_radius（大气半径） 换成了 bottom_radius（地球半径）。通过判别式来判断是否与地面相交或者计算射线长度。

积分计算光学长度 Optical Length 再计算 Transmittance

Length ComputeOpticalLengthToTopAtmosphereBoundary(DensityProfile profile, Length r, Number mu) 
{
  // Number of intervals for the numerical integration.
  const int SAMPLE_COUNT = 500;
  // The integration step, i.e. the length of each integration interval.
  Length dx = DistanceToTopAtmosphereBoundary(r, mu) / Number(SAMPLE_COUNT);
  // Integration loop.
  Length result = 0.0 * m;
  for (int i = 0; i <= SAMPLE_COUNT; ++i) 
  {
    Length d_i = Number(i) * dx;
    // Distance between the current sample point and the planet center.
    Length r_i = sqrt(d_i * d_i + 2.0 * r * mu * d_i + r * r);
    // Number density at the current sample point (divided by the number density
    // at the bottom of the atmosphere, yielding a dimensionless number).
    Number y_i = GetProfileDensity(profile, r_i - bottom_radius);
    // 梯形积分原则，首尾取0.5权重
    Number weight_i = i == 0 || i == SAMPLE_COUNT ? 0.5 : 1.0;
    result += y_i * weight_i * dx;
  }

  return result;
}

Transmittance=exp(−τ)，这里计算的是τ

在r、mu这个方向上的Optical Length等于路径上各点的积分

然后接着在下面使用上面的函数计算 Transmittance

DimensionlessSpectrum ComputeTransmittanceToTopAtmosphereBoundary(Length r, Number mu) 
{

  DimensionlessSpectrum density = 0;
  density += rayleigh_scattering * ComputeOpticalLengthToTopAtmosphereBoundary(RayleighDensity(), r, mu);
  density += mie_extinction * ComputeOpticalLengthToTopAtmosphereBoundary(MieDensity(), r, mu);
  density += absorption_extinction * ComputeOpticalLengthToTopAtmosphereBoundary(AbsorptionDensity(), r, mu);

  return exp(-density);
}

Transmittance=exp(−τ)，符合这个数学公式，把瑞利散射和米氏散射以及吸收量都计算，相加取负数再套上指数函数。

最终得到在r、mu下的Transmittance

后续

如果全写一篇会导致篇幅太长，于是分开写，后续会完成剩下预计算过程