本篇内容

// 计算透射度材质
            compute.Dispatch(compute_transmittance, CONSTANTS.TRANSMITTANCE_WIDTH / NUM_THREADS, CONSTANTS.TRANSMITTANCE_HEIGHT / NUM_THREADS, 1);
            // 计算没有经过任何散射的地面直接辐照度
            compute.Dispatch(compute_direct_irradiance, CONSTANTS.IRRADIANCE_WIDTH / NUM_THREADS, CONSTANTS.IRRADIANCE_HEIGHT / NUM_THREADS, 1);
            // 计算3D单次散射纹理
            for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer) 
            {
                // 计算3D texture ScatteringArray
                compute.SetInt("layer", layer);
                compute.Dispatch(compute_single_scattering, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
            }
            // 循环计算多次散射
            for (int scattering_order = 2; scattering_order <= num_scattering_orders; ++scattering_order) 
            {
                // 计算大气辐射度
                for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer) 
                {
                    compute.SetInt("layer", layer);
                    compute.Dispatch(compute_scattering_density, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
                }
                // 计算来自地面的辐照度
                compute.Dispatch(compute_indirect_irradiance, CONSTANTS.IRRADIANCE_WIDTH / NUM_THREADS, CONSTANTS.IRRADIANCE_HEIGHT / NUM_THREADS, 1);
                // 利用上面两项计算出本阶的多次散射
                for (int layer = 0; layer < CONSTANTS.SCATTERING_DEPTH; ++layer) 
                {
                    compute.SetInt("layer", layer);
                    compute.Dispatch(compute_multiple_scattering, CONSTANTS.SCATTERING_WIDTH / NUM_THREADS, CONSTANTS.SCATTERING_HEIGHT / NUM_THREADS, 1);
                }
            }

本篇主要讲解

• 大气辐射度

• 地面辐照度

• 和用以上两个材质计算的多次散射材质

第一步ComputeScatteringDensity

入口函数

#pragma kernel ComputeScatteringDensity
[numthreads(NUM_THREADS,NUM_THREADS,1)]
void ComputeScatteringDensity(uint3 id : SV_DispatchThreadID)
{
    id.z = layer;
    float3 gl_FragCoord = id + float3(0.5,0.5,0.5);

    float3 scattering_density = ComputeScatteringDensityTexture(transmittanceRead, singleRayleighScatteringRead,
                                singleMieScatteringRead, multipleScatteringRead,
                                irradianceRead, gl_FragCoord, scatteringOrder);

    deltaScatteringDensityWrite[id] = float4(scattering_density, 1);
}

RadianceDensitySpectrum ComputeScatteringDensityTexture(
    TransmittanceTexture transmittance_texture,
    ReducedScatteringTexture single_rayleigh_scattering_texture,
    ReducedScatteringTexture single_mie_scattering_texture,
    ScatteringTexture multiple_scattering_texture,
    IrradianceTexture irradiance_texture,
    float3 gl_frag_coord, int scattering_order) 
{
  Length r;
  Number mu;
  Number mu_s;
  Number nu;
  bool ray_r_mu_intersects_ground;
  GetRMuMuSNuFromScatteringTextureFragCoord(gl_frag_coord,
      r, mu, mu_s, nu, ray_r_mu_intersects_ground);

  return ComputeScatteringDensity(transmittance_texture,
      single_rayleigh_scattering_texture, single_mie_scattering_texture,
      multiple_scattering_texture, irradiance_texture, r, mu, mu_s, nu,
      scattering_order);
}

纹理映射函数GetRMuMuSNuFromScatteringTextureFragCoord上一章已经提到了，从gl坐标可以获取到我们需要的参数r, mu, mu_s, nu。

计算Radiance的原理

第一步，我们需要计算在大气中某一点 q 处，向某个方向 −ω 散射出的辐射度。假设这是第 n 次散射（bounce）。

这个 q 是散射点，最后会沿着 -ω 方向散射到我们的目标点 p 点，之后会对 -ω 这条线上的每一个这样的 q 点做直线积分。

这个 q 点的散射辐射度等于对所有可能的入射方向 ωᵢ 进行积分，也就是球面积分，积分的被积函数是以下的乘积：

• 从方向 ωᵢ 到达 q 处、经历了 n−1 次散射后的入射辐射度 Lᵢ，这部分包括以下的总和：

  • 第n-1阶预计算纹理给出的散射项

  • 此外，当射线[q, ωᵢ)与地面相交时，还要把这部分光路的贡献加上。因为我们预计算的多次散射纹理只包含在大气中发生的散射，不包括最后一次在地面上的反射；但这里地面反射后又在 q 处发生散射，所以必须单独计算。地面贡献等于：

    • q 到 相交点 之间的大气透射率；

    • 地面的平均反照率（albedo）；

    • Lambert漫反射BRDF（1/π）；

    • 地面在经历 n−2 次散射后接收到的辐照度；为什么是n-2呢，是因为这样说明第n-1次散射就有希望散射到 q 点，进而在第n次散射到目标点p

• 在 q 处的散射系数；

• 散射相位函数 p(ωᵢ→−ω)；

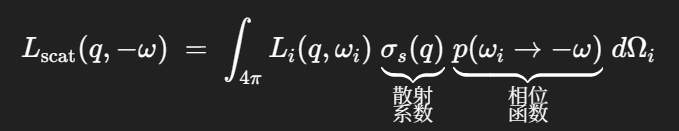
其中：

实现如下：

这里对 某一个 q 点的 所有 可能是入射方向 ωᵢ （也就是球面）做积分。（但不要忘了 之后还要对 每一个q 和每一个 -ω 做积分）

现在我们还只是单个计算L(q , -w)

RadianceDensitySpectrum ComputeScatteringDensity(
    TransmittanceTexture transmittance_texture,
    ReducedScatteringTexture single_rayleigh_scattering_texture,
    ReducedScatteringTexture single_mie_scattering_texture,
    ScatteringTexture multiple_scattering_texture,
    IrradianceTexture irradiance_texture,
    Length r, Number mu, Number mu_s, Number nu, int scattering_order) 
{

  // Compute unit direction vectors for the zenith, the view direction omega and
  // and the sun direction omega_s, such that the cosine of the view-zenith
  // angle is mu, the cosine of the sun-zenith angle is mu_s, and the cosine of
  // the view-sun angle is nu. The goal is to simplify computations below.
  float3 zenith_direction = float3(0.0, 0.0, 1.0);
  float3 omega = float3(sqrt(1.0 - mu * mu), 0.0, mu);
  Number sun_dir_x = omega.x == 0.0 ? 0.0 : (nu - mu * mu_s) / omega.x;
  Number sun_dir_y = sqrt(max(1.0 - sun_dir_x * sun_dir_x - mu_s * mu_s, 0.0));
  float3 omega_s = float3(sun_dir_x, sun_dir_y, mu_s);

  const int SAMPLE_COUNT = 16;
  const Angle dphi = pi / Number(SAMPLE_COUNT);
  const Angle dtheta = pi / Number(SAMPLE_COUNT);
  RadianceDensitySpectrum rayleigh_mie = RadianceDensitySpectrum(0,0,0);

  // Nested loops for the integral over all the incident directions omega_i.
  for (int l = 0; l < SAMPLE_COUNT; ++l) 
  {
    Angle theta = (Number(l) + 0.5) * dtheta;
    Number cos_theta = cos(theta);
    Number sin_theta = sin(theta);
    bool ray_r_theta_intersects_ground = RayIntersectsGround(r, cos_theta);

    // The distance and transmittance to the ground only depend on theta, so we
    // can compute them in the outer loop for efficiency.
    Length distance_to_ground = 0.0 * m;
    DimensionlessSpectrum transmittance_to_ground = DimensionlessSpectrum(0,0,0);
    DimensionlessSpectrum ground_albedo = DimensionlessSpectrum(0,0,0);
    if (ray_r_theta_intersects_ground) 
    {
      distance_to_ground = DistanceToBottomAtmosphereBoundary(r, cos_theta);
      transmittance_to_ground = GetTransmittance(transmittance_texture, r, cos_theta, distance_to_ground, true);
    }

    for (int m = 0; m < 2 * SAMPLE_COUNT; ++m) 
    {
      Angle phi = (Number(m) + 0.5) * dphi;
      float3 omega_i = float3(cos(phi) * sin_theta, sin(phi) * sin_theta, cos_theta);
      SolidAngle domega_i = (dtheta / rad) * (dphi / rad) * sin(theta) * sr;

      // The radiance L_i arriving from direction omega_i after n-1 bounces is
      // the sum of a term given by the precomputed scattering texture for the
      // (n-1)-th order:
      Number nu1 = dot(omega_s, omega_i);
      RadianceSpectrum incident_radiance = GetScattering(
          single_rayleigh_scattering_texture, single_mie_scattering_texture,
          multiple_scattering_texture, r, omega_i.z, mu_s, nu1,
          ray_r_theta_intersects_ground, scattering_order - 1);

      // and of the contribution from the light paths with n-1 bounces and whose
      // last bounce is on the ground. This contribution is the product of the
      // transmittance to the ground, the ground albedo, the ground BRDF, and
      // the irradiance received on the ground after n-2 bounces.
      float3 ground_normal = normalize(zenith_direction * r + omega_i * distance_to_ground);
      IrradianceSpectrum ground_irradiance = GetIrradiance(irradiance_texture, bottom_radius, dot(ground_normal, omega_s));
      incident_radiance += transmittance_to_ground * ground_albedo * (1.0 / (PI * sr)) * ground_irradiance;

      // The radiance finally scattered from direction omega_i towards direction
      // -omega is the product of the incident radiance, the scattering
      // coefficient, and the phase function for directions omega and omega_i
      // (all this summed over all particle types, i.e. Rayleigh and Mie).
      Number nu2 = dot(omega, omega_i);

      Number rayleigh_density = GetProfileDensity(RayleighDensity(), r - bottom_radius);
      Number mie_density = GetProfileDensity(MieDensity(), r - bottom_radius);

      rayleigh_mie += incident_radiance * (
          rayleigh_scattering * rayleigh_density * RayleighPhaseFunction(nu2) +
          mie_scattering * mie_density * MiePhaseFunction(mie_phase_function_g, nu2)) *
          domega_i;
    }
  }

  return rayleigh_mie;
}

首先准备几何向量，x、y坐标是水平面上的坐标，z是高度坐标。dω=sin⁡θ dθ dϕ 是立体角微元

得到omega，视线方向的归一化坐标，强制锁定其y坐标为0，作为太阳的参考物。得到omega_s，相对于视线方向的x、y坐标，和他的归一化高度z，也就是cos值mu_s。

球面积分原理

然后做入射方向的球面积分，但一个循环是从0到pi，另外一个是从0到2pi，从哪里看出来是球面？

首先看立体角的原理：

θ是天顶角，φ是方位角（经度）

或者你想想，一个半圆，绕着直径边旋转360°，就形成了一个球。

float3 omega_i = float3(
    cos(phi) * sin_theta,
    sin(phi) * sin_theta,
    cos_theta
);

这两个角通过映射得到单位笛卡尔坐标/向量

domega_i = sin(theta) * dtheta * dphi;

这里得到立体角微元

代码中：

• omega是某一个视线方向，对应公式中的 -ω；

• omega_s 是太阳方向

• omega_i 是积分过程中的某个方向，用于计算从这个方向散射过来的光

地面辐照度 ComputeIndirectIrradiance

这一部分的值被用在上一步，意义是第n-2次散射到地面的Irradiance，之后会在第n-1次被散射到q点

入口函数

#pragma kernel ComputeIndirectIrradiance
[numthreads(NUM_THREADS, NUM_THREADS, 1)]
void ComputeIndirectIrradiance(uint3 id : SV_DispatchThreadID)
{
    float2 gl_FragCoord = id.xy + float2(0.5,0.5);

    float3 delta_irradiance = ComputeIndirectIrradianceTexture(
                              singleRayleighScatteringRead,
                              singleMieScatteringRead, multipleScatteringRead,
                              gl_FragCoord, scatteringOrder);

    float3 irradiance = RadianceToLuminance(delta_irradiance);

    deltaIrradianceWrite[id.xy] = float4(delta_irradiance, 1);

    irradianceWrite[id.xy] = float4(irradiance, 1);

    if(blend[1] == 1)
       irradianceWrite[id.xy] += irradianceRead[id.xy];
}

各材质的意义

• deltaIrradianceWrite[id.xy] = float4(delta_irradiance, 1);

  • 本轮三个波长的累计地面辐照度。存储本次计算的“光谱辐照度增量”ΔE(λ)（对每组波长的离线果），是地面在当前散射阶中新产生的辐照度。

• irradianceWrite[id.xy] = float4(irradiance, 1);

  • 所有波长的累积地面辐照度。存储“累积亮度”Eₗᵤₘ（将 ΔE(λ) 按 CIE 亮度函数或 RGB 加权求和后的结果），并在 blend 开启时把历史结果（irradianceRead）累加进去，得到多阶最终地面亮度。

只有deltaIrradianceWrite会参与后续的计算

理论

对于间接地面辐照度，必须计算半球的积分。我们需要对半球上所有方向 ω 做积分，积分项是各方向上的乘积，即以下两项的乘积：

• 经过 n 次反射后到达方向 ω 的辐照度，

• 余弦因子，即 ωz

函数实现

IrradianceSpectrum ComputeIndirectIrradiance(
    ReducedScatteringTexture single_rayleigh_scattering_texture,
    ReducedScatteringTexture single_mie_scattering_texture,
    ScatteringTexture multiple_scattering_texture,
    Length r, Number mu_s, int scattering_order) 
{

  const int SAMPLE_COUNT = 32;
  const Angle dphi = pi / Number(SAMPLE_COUNT);
  const Angle dtheta = pi / Number(SAMPLE_COUNT);

  IrradianceSpectrum result = IrradianceSpectrum(0, 0, 0);

  float3 omega_s = float3(sqrt(1.0 - mu_s * mu_s), 0.0, mu_s);

  for (int j = 0; j < SAMPLE_COUNT / 2; ++j) 
  {
    Angle theta = (Number(j) + 0.5) * dtheta;

    for (int i = 0; i < 2 * SAMPLE_COUNT; ++i) 
    {
      Angle phi = (Number(i) + 0.5) * dphi;
      float3 omega = float3(cos(phi) * sin(theta), sin(phi) * sin(theta), cos(theta));
      SolidAngle domega = (dtheta / rad) * (dphi / rad) * sin(theta) * sr;
      Number nu = dot(omega, omega_s);

      result += GetScattering(single_rayleigh_scattering_texture,
                single_mie_scattering_texture, multiple_scattering_texture,
                r, omega.z, mu_s, nu, false,scattering_order) * omega.z * domega;
    }
  }

  return result;
}

辐照度（Irradiance）E 定义为从半球内各方向入射到点 P 上、乘以入射角余弦并对立体角积分后的辐射度

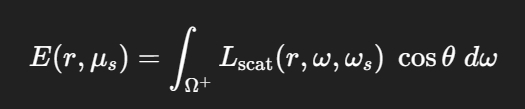
cosθ=ωz​ 是方向 ω 与法线方向的夹角余弦。dω=sin⁡θ dθ dϕ 是立体角微元

注意这里第一个循环是 j<SAMPLE_COUNT / 2，是九十度，其实是上半球积分

GetScattering函数：

• 一阶散射因为比较“简单”，把大气分子（Rayleigh）和气溶胶（Mie）分开存、分开算，再乘相位函数，精度高且贴图小。

• 多阶散射因为数据量大，直接把“密度×相位”结果烘焙到一个 3D 贴图里，运行时直接查表。

RadianceSpectrum GetScattering(
    ReducedScatteringTexture single_rayleigh_scattering_texture,
    ReducedScatteringTexture single_mie_scattering_texture,
    ScatteringTexture multiple_scattering_texture,
    Length r, Number mu, Number mu_s, Number nu,
    bool ray_r_mu_intersects_ground,
    int scattering_order) 
{
  if (scattering_order == 1) 
  {
    IrradianceSpectrum rayleigh = GetScattering(
        single_rayleigh_scattering_texture, r, mu, mu_s, nu,
        ray_r_mu_intersects_ground);

    IrradianceSpectrum mie = GetScattering(
        single_mie_scattering_texture, r, mu, mu_s, nu,
        ray_r_mu_intersects_ground);

    return rayleigh * RayleighPhaseFunction(nu) +
        mie * MiePhaseFunction(mie_phase_function_g, nu);
  } 
  else 
  {
    return GetScattering(
        multiple_scattering_texture, r, mu, mu_s, nu,
        ray_r_mu_intersects_ground);
  }
}

ComputeMultipleScattering

理论

这一步的核心是在视线方向 ω 上，对“沿射线每一点 q 处的散射贡献”做一次一维积分，这个散射贡献已经在ComputeScatteringDensity函数中计算完了。

入口函数

#pragma kernel ComputeMultipleScattering
[numthreads(NUM_THREADS, NUM_THREADS, 1)]
void ComputeMultipleScattering(uint3 id : SV_DispatchThreadID)
{
    id.z = layer;
    float3 gl_FragCoord = id + float3(0.5,0.5,0.5);

    float nu;
    float3 delta_multiple_scattering = ComputeMultipleScatteringTexture(
                                 transmittanceRead, deltaScatteringDensityRead,
                                 gl_FragCoord, nu);

    deltaMultipleScatteringWrite[id] = float4(delta_multiple_scattering, 1);

    scatteringWrite[id] = float4(RadianceToLuminance(delta_multiple_scattering) / RayleighPhaseFunction(nu), 0.0);

    if(blend[1] == 1)
       scatteringWrite[id] += scatteringRead[id];

}

具体实现

在ComputeMultipleScatteringTexture中，先进行纹理映射，然后调用ComputeMultipleScattering函数：

RadianceSpectrum ComputeMultipleScatteringTexture(
    TransmittanceTexture transmittance_texture,
    ScatteringDensityTexture scattering_density_texture,
    float3 gl_frag_coord, out Number nu) 
{
  Length r;
  Number mu;
  Number mu_s;
  bool ray_r_mu_intersects_ground;
  GetRMuMuSNuFromScatteringTextureFragCoord(gl_frag_coord,
      r, mu, mu_s, nu, ray_r_mu_intersects_ground);

  return ComputeMultipleScattering(transmittance_texture,
      scattering_density_texture, r, mu, mu_s, nu,
      ray_r_mu_intersects_ground);
}

RadianceSpectrum ComputeMultipleScattering(
    TransmittanceTexture transmittance_texture,
    ScatteringDensityTexture scattering_density_texture,
    Length r, Number mu, Number mu_s, Number nu,
    bool ray_r_mu_intersects_ground) 
{
  // Number of intervals for the numerical integration.
  const int SAMPLE_COUNT = 50;
  // The integration step, i.e. the length of each integration interval.
  Length dx = DistanceToNearestAtmosphereBoundary(r, mu, ray_r_mu_intersects_ground) / Number(SAMPLE_COUNT);

  // Integration loop.
  RadianceSpectrum rayleigh_mie_sum = RadianceSpectrum(0,0,0);

  for (int i = 0; i <= SAMPLE_COUNT; ++i) 
  {
    Length d_i = Number(i) * dx;

    // The r, mu and mu_s parameters at the current integration point (see the
    // single scattering section for a detailed explanation).
    Length r_i = ClampRadius(sqrt(d_i * d_i + 2.0 * r * mu * d_i + r * r));
    Number mu_i = ClampCosine((r * mu + d_i) / r_i);
    Number mu_s_i = ClampCosine((r * mu_s + d_i * nu) / r_i);

    // The Rayleigh and Mie multiple scattering at the current sample point.
    RadianceSpectrum rayleigh_mie_i =
        GetScattering(scattering_density_texture, r_i, mu_i, mu_s_i, nu, ray_r_mu_intersects_ground) *
        GetTransmittance(transmittance_texture, r, mu, d_i, ray_r_mu_intersects_ground) * dx;

    // Sample weight (from the trapezoidal rule).
    Number weight_i = (i == 0 || i == SAMPLE_COUNT) ? 0.5 : 1.0;
    rayleigh_mie_sum += rayleigh_mie_i * weight_i;
  }

  return rayleigh_mie_sum;
}

这是沿着直线做积分，注意上次的ComputeDensity是做球面积分。

最后得到的delta_multiple_scattering 就是rayleigh_mie_sum的值。

预告

下一篇会分享实际的渲染Shader的学习心得，有关如何形成光锥尾影、如何使用这些材质等。