函数们

求太阳可见度

float GetSunVisibility(float3 _point, float3 sun_direction)
{
    float3 p = _point - kSphereCenter;
    float p_dot_v = dot(p, sun_direction);
    float p_dot_p = dot(p, p);
    float ray_sphere_center_squared_distance = p_dot_p - p_dot_v * p_dot_v;
    float distance_to_intersection = -p_dot_v - sqrt(max(0.0, kSphereRadius * kSphereRadius - ray_sphere_center_squared_distance));
 
    if (distance_to_intersection > 0.0) 
    {
       // Compute the distance between the view ray and the sphere, and the
       // corresponding (tangent of the) subtended angle. Finally, use this to
       // compute an approximate sun visibility.
       float ray_sphere_distance = kSphereRadius - sqrt(ray_sphere_center_squared_distance);
       float ray_sphere_angular_distance = -ray_sphere_distance / p_dot_v;
 
       return smoothstep(1.0, 0.0, ray_sphere_angular_distance / sun_size.x);
    }
 
    return 1.0;
}

我画一个几何来表示上面在干什么：

p1,p2,p3是三种不同情况下的视线点，只有p3会形成遮挡

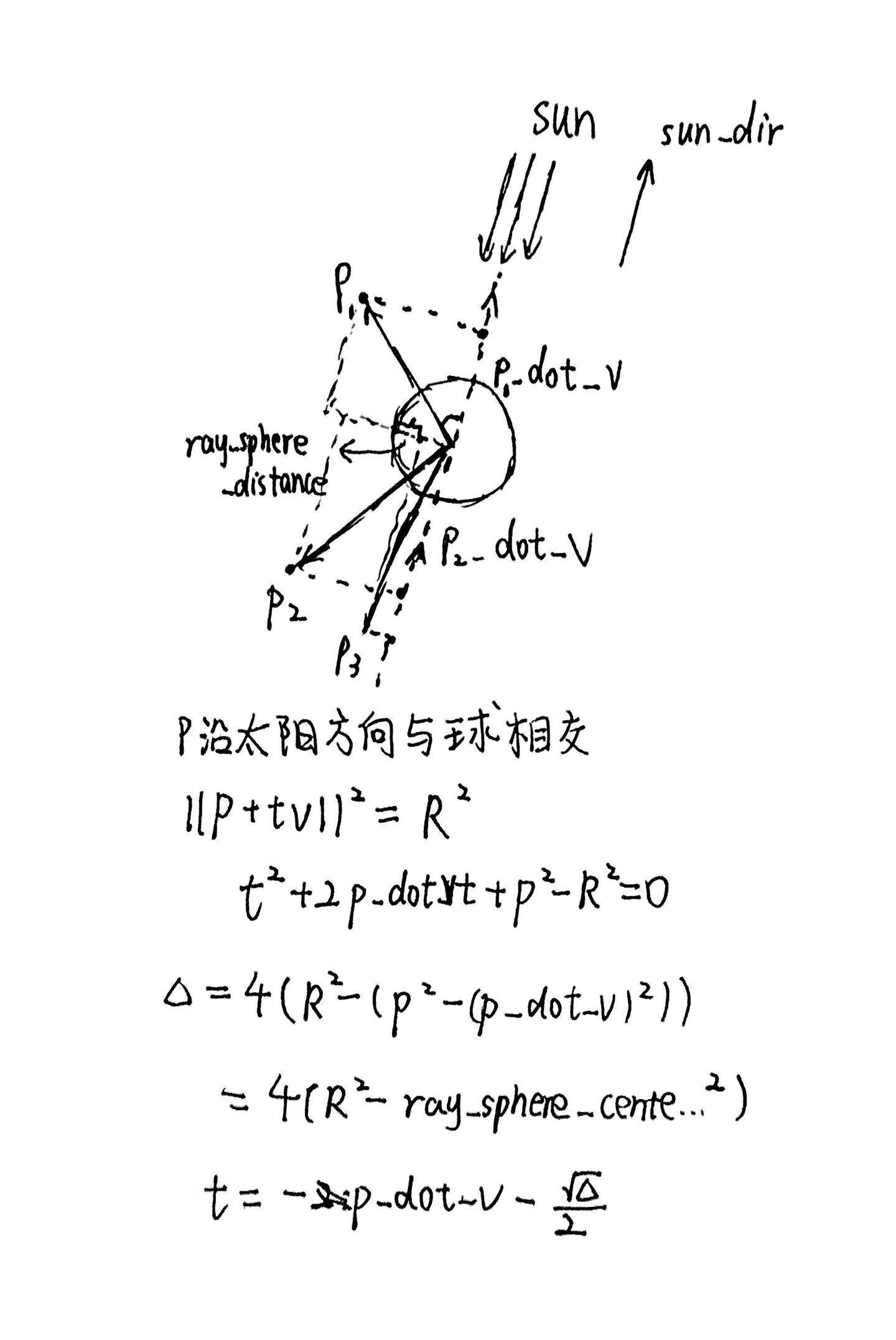
最后的float ray_sphere_angular_distance = -ray_sphere_distance / p_dot_v;本质上是求ray_sphere_distance 和p_dot_v形成的直角三角形的某一个角的tan值。

然后再除以sun_size.x（这里的sun_size.x是Mathf.Tan(kSunAngularRadius)），也是一个tan值，得到球是否完全覆盖太阳盘，形成软阴影。

天空可见度

球也可以遮挡住部分天空，这里的可见度也需要计算

球体引起的环境光衰减因子由辐射视因子（Isidoro Martinez, 1995）给出。在球体完全可见的简单情况下，天空可见度由以下函数给出：

float GetSkyVisibility(float3 _point) 
{
    float3 p = _point - kSphereCenter;
    float p_dot_p = dot(p, p);
    return 1.0 + p.y / sqrt(p_dot_p) * kSphereRadius * kSphereRadius / p_dot_p;
}

公式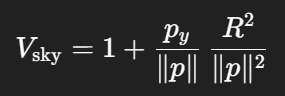

光柱

void GetSphereShadowInOut(float3 view_direction, float3 sun_direction, out float d_in, out float d_out)
{
    float3 camera = _WorldSpaceCameraPos;
    float3 pos = camera - kSphereCenter;
    float pos_dot_sun = dot(pos, sun_direction);
    float view_dot_sun = dot(view_direction, sun_direction);
    float k = sun_size.x;  //Mathf.Tan(kSunAngularRadius)
    float l = 1.0 + k * k;
    float a = 1.0 - l * view_dot_sun * view_dot_sun;
    float b = dot(pos, view_direction) - l * pos_dot_sun * view_dot_sun -
       k * kSphereRadius * view_dot_sun;
    float c = dot(pos, pos) - l * pos_dot_sun * pos_dot_sun -
       2.0 * k * kSphereRadius * pos_dot_sun - kSphereRadius * kSphereRadius;
    float discriminant = b * b - a * c;
    if (discriminant > 0.0) 
    {
       d_in = max(0.0, (-b - sqrt(discriminant)) / a);
       d_out = (-b + sqrt(discriminant)) / a;
       // The values of d for which delta is equal to 0 and kSphereRadius / k.
       float d_base = -pos_dot_sun / view_dot_sun;
       float d_apex = -(pos_dot_sun + kSphereRadius / k) / view_dot_sun;
 
       if (view_dot_sun > 0.0) 
       {
          d_in = max(d_in, d_apex);
          d_out = a > 0.0 ? min(d_out, d_base) : d_base;
       }
       else 
       {
          d_in = a > 0.0 ? max(d_in, d_base) : d_base;
          d_out = min(d_out, d_apex);
       }
    }
    else 
    {
       d_in = 0.0;
       d_out = 0.0;
    }
}

由于太阳不是点光源（α 为太阳的角半径），阴影体积不是一个圆柱，而是一个圆锥

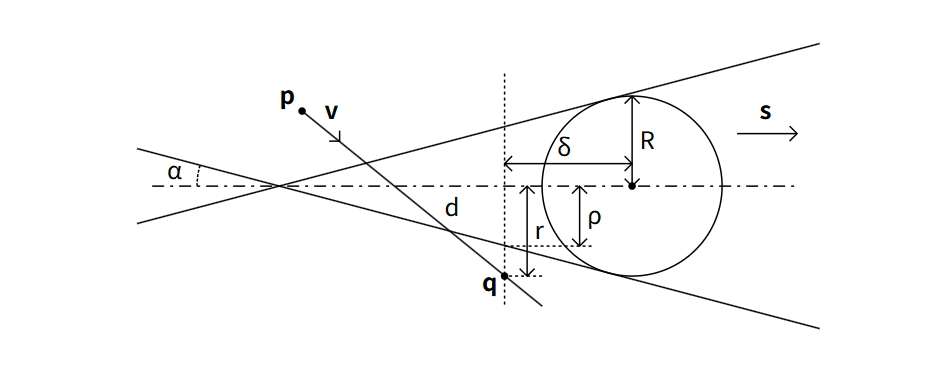
如上图所示，以圆心为0坐标点，p 为相机位置，v 和 s 分别为单位视线向量和太阳方向向量，R 为球体半径(假设球心位于原点)。距离相机 d 的点为 q = p+ dv。该点沿本影圆锥轴方向距离球心 δ =-q·s，偏离该轴的距离由r 给出。最终，在轴方向距离处，本影圆锥的半径为ρ= R－tanα，其中 α 为太阳的角半径。距离相机 d 的点位于阴影圆锥上，当且仅当r² = ρ² 时:

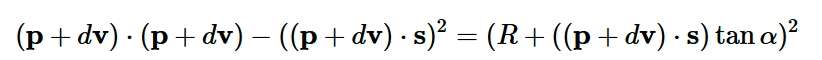
展开后，可以得到d的二次方程：

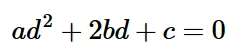
其中：

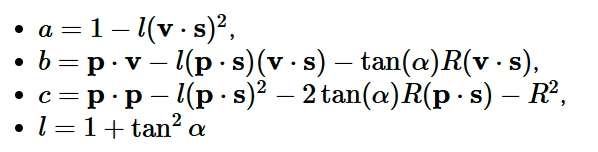
太阳直射和天空散射

IrradianceSpectrum GetSunAndSkyIrradiance(
    TransmittanceTexture transmittance_texture,
    IrradianceTexture   irradiance_texture,
    Position            pos,
    Direction           normal,
    Direction           sun_direction,
    out IrradianceSpectrum sky_irradiance)
{
    // 1) 先算出当前点到星心（地心）距离 r
    Length r = length(pos);
 
    // 2) mu_s = cos(太阳天顶角) = (p·s) / |p|
    Number mu_s = dot(pos, sun_direction) / r;
 
    // 3) 【漫散射（Indirect）部分】从预计算的 irradiance 2D 纹理里查
    //    GetIrradiance(irradiance_texture, r, mu_s) 本身就是
    //      ∫L_sky(θ,φ)·cosθ ·dω
    //    但那个是针对“水平面”的辐照，我们对任意法线加个近似修正：
    //      * (1 + cos θ_surface)/2
    //    其中 cos θ_surface = dot(normal, pos)/r  表面法线与“上正方向”(pos) 的夹角余弦
    sky_irradiance = GetIrradiance(irradiance_texture, r, mu_s)
                   * (1.0 + dot(normal, pos)/r) * 0.5;
 
    // 4) 【直射（Direct）部分】
    //    solar_irradiance —— 顶层大气的太阳谱辐照度 (W/m²)
    //    GetTransmittanceToSun(...) —— 从 p 看向太阳方向的衰减 (0–1)
    //    max(dot(normal, sun_direction),0) —— Lambert 面对太阳法线余弦项
    //
    //    结果就是传出的“直射辐照度”：
    return solar_irradiance
         * GetTransmittanceToSun(transmittance_texture, r, mu_s)
         * max(dot(normal, sun_direction), 0.0);
}

DimensionlessSpectrum GetTransmittanceToSun(TransmittanceTexture transmittance_texture, Length r, Number mu_s) 
{
  Number sin_theta_h = bottom_radius / r;
  Number cos_theta_h = -sqrt(max(1.0 - sin_theta_h * sin_theta_h, 0.0));
 
  Number step = smoothstep(-sin_theta_h * sun_angular_radius / rad, sin_theta_h * sun_angular_radius / rad, mu_s - cos_theta_h);
 
  return GetTransmittanceToTopAtmosphereBoundary(transmittance_texture, r, mu_s) * step;
      
}

RenderSky

/// <summary>
/// 计算沿视线 (view_ray) 在大气层中所看到的天空散射辐射，并输出从摄像机到大气顶端的透射率。
/// 基于 Bruneton & Neyret 《Precomputed Atmospheric Scattering》模型实现。
/// </summary>
RadianceSpectrum GetSkyRadiance(
    TransmittanceTexture transmittance_texture,            // 预计算透射率纹理
    ReducedScatteringTexture scattering_texture,           // 预计算多次散射纹理
    ReducedScatteringTexture single_mie_scattering_texture,// 预计算单次 Mie 散射纹理
    Position camera,           // 摄像机位置（以地心为原点的世界坐标）
    Direction view_ray,        // 视线方向（单位向量）
    Length shadow_length,      // 光柱（光轴）特效，需要跳过的初始散射长度（无特效时为 0）
    Direction sun_direction,   // 太阳方向（单位向量）
    out DimensionlessSpectrum transmittance // 输出：摄像机到大气顶端的透射率
)
{
    //====================================================
    // 1. 处理摄像机在大气层外的情况 
    //====================================================
    Length r   = length(camera);                   // 摄像机到地心的距离 r
    Length rmu = dot(camera, view_ray);            // 视线方向与 camera 向量的投影长度 r·μ

    // 计算视线与大气最外层（半径 top_radius）的交点距离 t
    // 解射线—球相交方程：t^2 + 2*rmu*t + (r^2 - top_radius^2) = 0
    Length distance_to_top_atmosphere_boundary =
        -rmu - sqrt(rmu*rmu - r*r + top_radius*top_radius);

    // 如果摄像机在大气层外并且视线会进入大气
    if (distance_to_top_atmosphere_boundary > 0.0 * m)
    {
        // 将观察点沿视线移动到大气顶端，方便后续统一为大气内部计算
        camera = camera + view_ray * distance_to_top_atmosphere_boundary;
        r = top_radius;                               // 更新半径 r 为大气顶端半径
        rmu += distance_to_top_atmosphere_boundary;   // 更新投影长度 r·μ
    }
    else if (r > top_radius)
    {
        // 如果摄像机在大气外且视线不穿入大气，则没有散射，完全透射
        transmittance = DimensionlessSpectrum(1, 1, 1);
        return RadianceSpectrum(0, 0, 0);
    }

    //====================================================
    // 2. 计算纹理查找所需的参数 (r, μ, μ_s, ν)
    //====================================================
    Number mu   = rmu / r;                          // μ = cos(theta_v)：视线与径向的余弦
    Number mu_s = dot(camera, sun_direction) / r;   // μ_s = cos(theta_s)：太阳方向与径向的余弦
    Number nu   = dot(view_ray, sun_direction);     // ν = cos(phi)：视线与太阳方向的余弦
    bool ray_r_mu_intersects_ground = RayIntersectsGround(r, mu);

    //====================================================
    // 3. 获取从摄像机到大气顶端的总透射率 T(r, μ)
    //====================================================
    if (ray_r_mu_intersects_ground)
    {
        // 如果视线会击中地面，透射率为零
        transmittance = DimensionlessSpectrum(0, 0, 0);
    }
    else
    {
        // 否则从预计算透射纹理中查表
        transmittance = GetTransmittanceToTopAtmosphereBoundary(
            transmittance_texture, r, mu);
    }

    //====================================================
    // 4. 计算散射贡献
    //    包含 Rayleigh + 多次 Mie 散射，以及单次 Mie 散射
    //====================================================
    IrradianceSpectrum single_mie_scattering;       // 用于存储单次 Mie 散射
    IrradianceSpectrum scattering;                  // 存储总散射辐照度

    if (shadow_length == 0.0 * m)
    {
        // 普通情况：无光柱特效，直接查 Rayleigh+Mie 散射合并结果
        scattering = GetCombinedScattering(
            scattering_texture,
            single_mie_scattering_texture,
            r, mu, mu_s, nu,
            ray_r_mu_intersects_ground,
            single_mie_scattering);
    }
    else
    {
        // 光柱特效：跳过前段散射，参考论文公式 (18)
        Length d = shadow_length;                    // 需要跳过的散射起点距离
        // 计算跳过后位置的半径 r_p 与余弦 μ_p, μ_s_p
        Length r_p = ClampRadius(
            sqrt(d*d + 2.0*r*mu*d + r*r));
        Number mu_p   = (r*mu + d) / r_p;
        Number mu_s_p = (r*mu_s + d*nu) / r_p;

        // 在新位置调用相同散射查表
        scattering = GetCombinedScattering(
            scattering_texture,
            single_mie_scattering_texture,
            r_p, mu_p, mu_s_p, nu,
            ray_r_mu_intersects_ground,
            single_mie_scattering);

        // 计算前段阴影区间的透射率并乘到散射值上
        DimensionlessSpectrum shadow_transmittance =
            GetTransmittance(
                transmittance_texture,
                r, mu,
                shadow_length,
                ray_r_mu_intersects_ground);

        scattering          *= shadow_transmittance;
        single_mie_scattering *= shadow_transmittance;
    }

    //====================================================
    // 5. 按相函数加权并输出最终天空辐射
    //====================================================
    // 瑞利相函数加权
    RadianceSpectrum rayleigh_part = scattering * RayleighPhaseFunction(nu);
    // Mie 相函数加权单次 Mie 散射
    RadianceSpectrum mie_part     = single_mie_scattering * MiePhaseFunction(mie_phase_function_g, nu);

    // 两者相加并返回
    return rayleigh_part + mie_part;
}

讲解一下

这里的

// 如果摄像机在大气层外并且视线会进入大气

if (distance_to_top_atmosphere_boundary > 0.0 * m)

这里计算的二次方程的根，是取小的那一个根，也就是说，如果相机在内部，那么根一定是小于0的。

若t大于0，视线与大气顶端的交点在相机前方，所以视线一定是从外面射入进来的。

以及

Length d = shadow_length; Length r_p = ClampRadius(sqrt(d d + 2.0 r mu d + r r));

Number mu_p = (r mu + d) / r_p; Number mu_s_p = (r mu_s + d nu) / r_p;

是把相机往前移动了shadow_length后的新坐标

设置Rendertexture顶点

float CAMERA_FOV = camera.fieldOfView;
float CAMERA_ASPECT_RATIO = camera.aspect;
float CAMERA_NEAR = camera.nearClipPlane;
float CAMERA_FAR = camera.farClipPlane;
 
Matrix4x4 frustumCorners = Matrix4x4.identity;
 
float fovWHalf = CAMERA_FOV * 0.5f;
 
Vector3 toRight = camera.transform.right * CAMERA_NEAR * Mathf.Tan(fovWHalf * Mathf.Deg2Rad) * CAMERA_ASPECT_RATIO;
Vector3 toTop = camera.transform.up * CAMERA_NEAR * Mathf.Tan(fovWHalf * Mathf.Deg2Rad);
 
Vector3 topLeft = (camera.transform.forward * CAMERA_NEAR - toRight + toTop);
float CAMERA_SCALE = topLeft.magnitude * CAMERA_FAR / CAMERA_NEAR;
 
topLeft.Normalize();
topLeft *= CAMERA_SCALE;
 
Vector3 topRight = (camera.transform.forward * CAMERA_NEAR + toRight + toTop);
topRight.Normalize();
topRight *= CAMERA_SCALE;
 
Vector3 bottomRight = (camera.transform.forward * CAMERA_NEAR + toRight - toTop);
bottomRight.Normalize();
bottomRight *= CAMERA_SCALE;
 
Vector3 bottomLeft = (camera.transform.forward * CAMERA_NEAR - toRight - toTop);
bottomLeft.Normalize();
bottomLeft *= CAMERA_SCALE;
 
frustumCorners.SetRow(0, topLeft);
frustumCorners.SetRow(1, topRight);
frustumCorners.SetRow(2, bottomRight);
frustumCorners.SetRow(3, bottomLeft);
 
m_material.SetMatrix("frustumCorners", frustumCorners);
 
CustomGraphicsBlit(src, dest, m_material, 0);

在 shader 里，你会把这个 frustumCorners 矩阵拿去重建每个像素对应的世界空间视线（view ray）。举

在顶点着色器里，把这个矩阵传给插值器： o.view_ray = frustumCorners[index].xyz;

然后在片元着色器里 normalize(o.view_ray) 就得到了 // 从摄像机出发、通过该像素的世界空间方向向量

片元着色器

GPT Summary：

fixed4 frag(v2f i) : SV_Target
{
    // 摄像机世界空间位置
    float3 camera = _WorldSpaceCameraPos;
    // 视线方向（归一化）
    float3 view_direction = normalize(i.view_ray);
    // 片元在屏幕空间的“角大小”，用于后续对小物体的抗锯齿处理
    float fragment_angular_size = length(ddx(i.view_ray) + ddy(i.view_ray)) / length(i.view_ray);

    // 计算视线穿过“太阳球”阴影体时的入口和出口距离
    float shadow_in, shadow_out;
    GetSphereShadowInOut(view_direction, sun_direction, shadow_in, shadow_out);

    // 当太阳接近地平线时，衰减光柱
    float lightshaft_fadein_hack = smoothstep(
        0.02, 0.04,
        dot(normalize(camera - earth_center), sun_direction)
    );

    // ==========================
    // —— 太阳球 (Sphere S) 部分 ——  
    // ==========================
    float3 p = camera - kSphereCenter;
    float p_dot_v = dot(p, view_direction);
    float p_dot_p = dot(p, p);
    // 光线到太阳球中心的最短距离的平方
    float ray_sphere_center_squared_distance = p_dot_p - p_dot_v * p_dot_v;
    // 计算视线与球体交点距离（可能为 NaN）
    float distance_to_intersection = -p_dot_v
        - sqrt(kSphereRadius * kSphereRadius - ray_sphere_center_squared_distance);

    float sphere_alpha = 0.0;
    float3 sphere_radiance = float3(0,0,0);
    if (distance_to_intersection > 0.0)
    {
        // 交点处到球面表面的距离，用于求“角距离”
        float ray_sphere_distance = kSphereRadius - sqrt(ray_sphere_center_squared_distance);
        float ray_sphere_angular_distance = -ray_sphere_distance / p_dot_v;
        // 近似的球体抗锯齿 alpha
        sphere_alpha = min(ray_sphere_angular_distance / fragment_angular_size, 1.0);

        // 计算交点坐标及法线
        float3 _point = camera + view_direction * distance_to_intersection;
        float3 normal = normalize(_point - kSphereCenter);

        // 计算该点的天空和太阳辐照度
        float3 sky_irradiance;
        float3 sun_irradiance = GetSunAndSkyIrradiance(
            _point - earth_center, normal, sun_direction, sky_irradiance);

        // 利用朗伯 BRDF 计算反射辐射
        sphere_radiance = kSphereAlbedo * (1.0 / PI) * (sun_irradiance + sky_irradiance);

        // 考虑大气透射与多次散射
        float shadow_length = max(0.0,
            min(shadow_out, distance_to_intersection) - shadow_in)
            * lightshaft_fadein_hack;

        float3 transmittance;
        float3 in_scatter = GetSkyRadianceToPoint(
            camera - earth_center, _point - earth_center,
            shadow_length, sun_direction, transmittance);

        // 混合透射与入射散射
        sphere_radiance = sphere_radiance * transmittance + in_scatter;
    }

    // ==========================
    // —— 地面 (Planet P) 部分 ——  
    // ==========================
    p = camera - earth_center;
    p_dot_v = dot(p, view_direction);
    p_dot_p = dot(p, p);
    // 光线到地心的最短距离的平方
    float ray_earth_center_squared_distance = p_dot_p - p_dot_v * p_dot_v;
    distance_to_intersection = -p_dot_v
        - sqrt(earth_center.y * earth_center.y - ray_earth_center_squared_distance);

    float ground_alpha = 0.0;
    float3 ground_radiance = float3(0,0,0);
    if (distance_to_intersection > 0.0)
    {
        // 交点及法线
        float3 _point = camera + view_direction * distance_to_intersection;
        float3 normal = normalize(_point - earth_center);

        // 计算天空与太阳辐照度
        float3 sky_irradiance;
        float3 sun_irradiance = GetSunAndSkyIrradiance(
            _point - earth_center, normal,
            sun_direction, sky_irradiance);

        // 计算太阳可见度和天空可见度
        float sunVis = GetSunVisibility(_point, sun_direction);
        float skyVis = GetSkyVisibility(_point);

        // 朗伯 BRDF 地面反射
        ground_radiance = kGroundAlbedo * (1.0 / PI)
            * (sun_irradiance * sunVis + sky_irradiance * skyVis);

        // 大气透射与入射散射
        float shadow_length = max(0.0,
            min(shadow_out, distance_to_intersection) - shadow_in)
            * lightshaft_fadein_hack;

        float3 transmittance;
        float3 in_scatter = GetSkyRadianceToPoint(
            camera - earth_center, _point - earth_center,
            shadow_length, sun_direction, transmittance);

        ground_radiance = ground_radiance * transmittance + in_scatter;
        ground_alpha = 1.0; // 地面总是全不透明
    }

    // ==========================
    // —— 天空散射与合成 ——  
    // ==========================
    float shadow_length = max(0.0, shadow_out - shadow_in) * lightshaft_fadein_hack;
    float3 transmittance;
    // 计算纯天空散射辐射
    float3 radiance = GetSkyRadiance(
        camera - earth_center, view_direction,
        shadow_length, sun_direction, transmittance);

    // 如果直接看向太阳方向，叠加太阳光辐射
    if (dot(view_direction, sun_direction) > sun_size.y)
    {
        radiance += transmittance * GetSolarRadiance();
    }

    // 按照从远到近：天空 → 地面 → 太阳球 进行混合（前景覆盖后景）
    radiance = lerp(radiance, ground_radiance, ground_alpha);
    radiance = lerp(radiance, sphere_radiance, sphere_alpha);

    // 曝光与伽马校正
    radiance = pow(1.0 - exp(-radiance / white_point * exposure), 1.0 / 2.2);

    return float4(radiance, 1);
}

这段 frag 着色器函数主要模拟了大气散射、地面与“太阳球”反射、以及光柱（光轴）等多种现象，通过光线投射与物理基的 BRDF 计算，将天空、地面、太阳球三者分层渲染后再进行前向混合，最终再加上曝光和伽马校正，以获得既具有真实感又抗锯齿的成像效果。它综合了：

• 阴影与光柱：GetSphereShadowInOut 结合视线与球体阴影区间计算，并用 lightshaft_fadein_hack 对地平线附近光柱进行淡入淡出处理。

• 大气透射与散射：用 GetSkyRadianceToPoint 和 GetSkyRadiance 分别计算直接与间接散射，模拟大气色彩与深度感。

• 朗伯反射：对地面和太阳球都使用 (1/PI) * Albedo * Irradiance 的简单朗伯模型，满足物理感知的反射分布。

• 多层合成：先天空、后地面、最后太阳球的前向混合，可保证近景覆盖远景。

• 后处理：线性空间之辐射值通过 1 - exp(-x) 曝光模型映射到显示空间，并做 2.2 伽马校正。